When the range of imperfection is localized to the vicinity of only a few atoms it is called as point defect or point imperfection.

Vacancy, Interstitial and Impurity atom :
The vacancy is formed by the removal of an atom from an atomic site and the interstitial by the introduction of an atom into a non-lattice site position.
The term impurity denotes a foreign aom existing in a parent metal lattice.

Frenkel Defect :
Frenkel Defect is formed when an atom (better to say ion, especially cation) leaves its original lattice site and occupies an interstitial position on the same crystal. Usually, this type of defect is observed in ionic solids, where size of anion is substantially larger than the size of cation. No change in density of material.
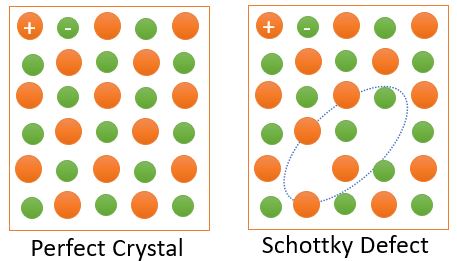
Shottkey Defect :
Schottky defect formed when oppositely charged atoms (anion and cation) leave their corresponding lattice sites and leave a pair of Vacancy Defects. Since both anion and cation leave the lattice sites at the same time, so overall electrical neutrality of the crystal is maintained; however, density of material reduces because of the vacancies. Schottky defects occur in ionic crystals where the size of anion is almost same with the size of the cation.

---

Calculation of number Equilibrium Vacancy
At equilibrium, the fraction of lattice that are vacant at a given temperature is given approximately by the equation.

\[ \boxed{ \frac{n}{N} = e^{-\frac{E_{s}}{kT}} } \]

Where n is the number of vacant sites in N sites and \( E_{s} \) is the energy required to move an atom from interior site to surface.

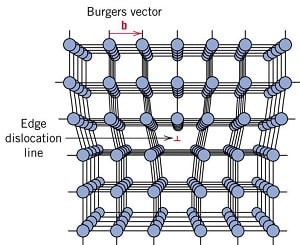
Two dimensional defects are most important as these defects are responsible for the phenomenon of slip. These defects is called dislocation, which can be define as a boundary between a slipped and unslipped portion of a crystal.And these 1-D defects are also known as linear defects.
Burger's Vector : The movement of dislocation in a lattice is charecterised by burger's vector. It indicates the magnitude and direction of movement of dislocation.
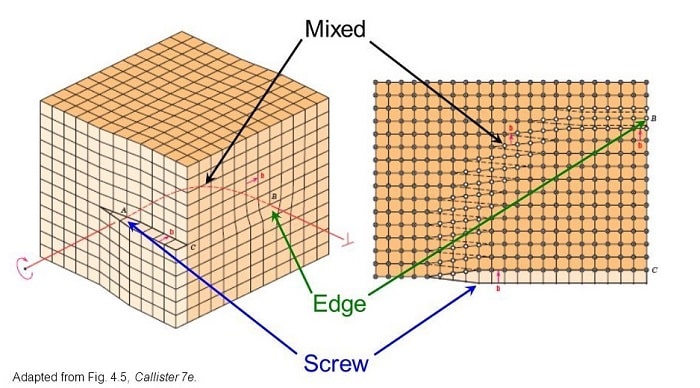
Energy required for doslocation movement : \[ \boxed{E_{b} =\frac{Gb^2}{2}} \] Type of Linear defects :
        (a) Edge Dislocation
        (b) Screw Dislocation
        (c) Mixed Dislocation

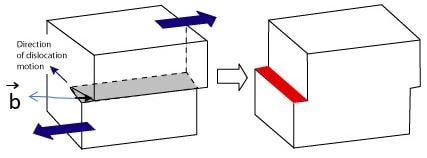
Edge Dislocation :
• An edge dislocation can be visualised as where an extra half-plane of atoms is inserted midway through the crystal lattice,and distorting nearby planes of atoms.
• The Burger's vector (𝑏) of Edge Dislocation is perpendicular (⊥) to its dislocation line.
• The figure below shows an edge dislocation. Edge dislocation is denoted by ⊥
Screw Dislocation :
• A screw dislocation can be visualized as the lattice structure of a crystal in which the atomic planes arranged in a helical pattern around a dislocation line.
• The Burger's vector (𝑏) of Screw Dislocation is Parallel (||) to its dislocation line.
• The figure below shows an screw dislocation. Screw dislocation is denoted by ↻
Mixed Dislocation :
• The mixed dislocation are neither pure edge nor pure screw dislocation.
• Thry consisting of both screw and edge character.
• The Burger's vector (𝑏) of screw Dislocation is neither perpendicular (⊥) nor parallel (||) to its dislocation line.

Difference between Edge and screw dislocation :

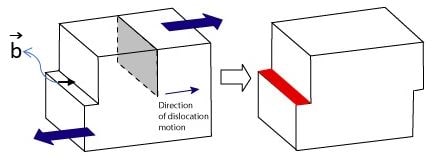
Dislocation Property	Edge	Screw
Relation of b and dislocation line	Perpendicular	Parallel
Slip Direction	Parallel to b	Parallel to b
Movement of Dislocation Line W.r.t. b	Parallel	Perpendicular
Leaves plane by	climb	Cross-Slip

Grain Boundaries :
Grain Boundaries formed when two randomly growing solid phases meets a junction. These phases are of same crystal but the orientation of grains differ.
Properties of GBs :
(1) GBs are the regions of orientation mis-match
(2) GBs are the regions of high energy
(3) GBs have low melting point (Solidify at last)
(4) GBs have high conc. of impurities
(5) Amrphous Region

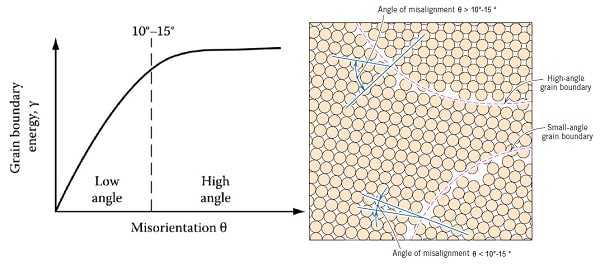
High angle Grain Boundary :
• When \( \theta > 10-15^\circ \) the boundary is known as a random high angle grain boundary.
• In general, when \( \theta > 10-15^\circ \) the dislocation spacing is so small that the dislocation cores overlap and it is then impossible to physically identify the individual dislocations
• At this stage the grain boundary energy is almost independent of misorientation
Low angle Grain Boundary :
• When \( \theta < 10-15^\circ \) the boundary is known as a random low angle grain boundary.

Low angle Tilt Grain Boundaries :
• The low angle tilt boundary is an array of parallel edge dislocations (i.e., Two or more edge dislocatios existing one above the other.)
• The tilt boundary need not be symmetrical with respect to the two adjoining crystals.

\[ \textrm{Angle of Tilt }(\theta) = \frac{b}{h} \] Where b = Burger vector , h = Ang. spacing b/w dislocation

Low angle Twist Grain Boundaries :
• The twist boundary is a cross grid of two sets of screw dislocations
\[ \textrm{Angle of Twist }(\alpha) = \frac{b}{h} \] Where b = Burger vector , h = Ang. spacing b/w dislocation

Twin Boundaries :