Dispersion Strengthening

Dispersion strengthening refers to the process of increasing the strength of a material by introducing uniform dispersion of second phase particles through the addition of an alloying element, which inhibits the motion of dislocations

Presence of small particles of a second phase and, if dispersed in a matrix can remarkably increase the matrix yield strength even when the dispersoid volume fraction is low. This is so because an aggregate of solute atoms resists dislocation motion to a considerably greater extent than does an isolated solute atom. The second phase particles in dispersion-hardened alloy has very little solubility in the matrix even at elevated temperature and have no coherency between the secong phase particle and matrix. hence, offer much more resistance to dislocation than precipitation hardening.

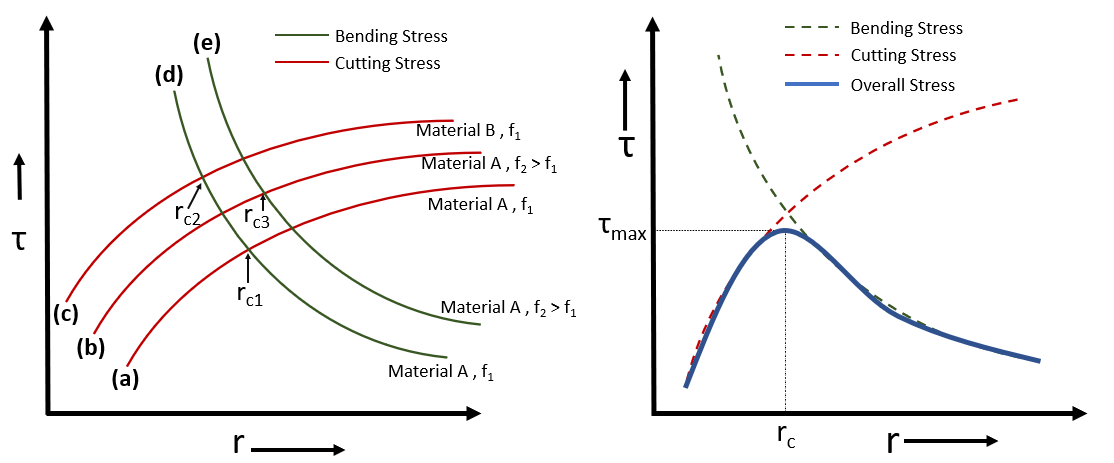
Dispersion strengthening depends on a number of factors. These include the size, volume fraction and elastic modulus of the dispersed particles. The volume fraction can also be defined in term of L, i.e., average distance between two particles. The stress required to force the dislocation through obstacles / 2^nd phase partocles is -
\[ \tau = \frac{Gb}{L} \] Here,
\( \tau \) : Stress required to bend dislocation between two particle
G : Shear modulus
b : Burger's vector
L : Distance between the particles

---

Interaction of a moving dislocation with dispersed particle :

Closely spaced fine particles obstruct the motion of dislocations moving in the matrix. A moving dislocation has two options to pass through dispersion particles as -

1. Cut through the precipitates :
Cutting through the precipitate particles become predominent when the precipitate particles are coherent with the matrix, have less elastic modulus than matrix or precipitates have very less size i.e., less than 50 Å . The increased resistance to dislocation motion in cutting through the particles is due to the creation of a step at the interface as shown in figure. A dislocation line (t) having a burger vector 'b' cut through precipitate as moves along.


• Precipitates with large radius are difficult to cut hence, requires more stress to move dislocation and vice versa.
• Increasing volume fraction \(f \), of solute also makes it difficult to cut precipitate
• Solute having high elastic modulus than the matrix significantly increase the stress required to cut through precipitates. Means higher the elastic modulus of solute higher will be the dispersion strenghening.


2. Bend aroung and bypass the precipitates (Orowan's looping) :
When the precipitates size are large (like 100 -500 Å ) or siffer, then instead of cutting through precipitate, the dislocation prefer to bend aroung and bypass them. This phenomenon was described by the Orowan mechanism.. The above figure (a), show a straight dislotaction line (t) having burger vector 'b' approching to two particles seperated by distance 'L'. In figure (b), on application of stress the line beginning to bend and contineous to bend till it reaches a critical radius (fig (c)), and stress required to bow the dislocation line b/w these two particles will be - \[ \boxed{ \tau = \frac{Gb}{L} } \] After this point dislocation will start bulging out and the segments of dislocation will meet (or annihilate, as dislocations will be of opposite sign on other side) on other side of the particle. leaving a dislocation loop around each particle (fig. (d)). And then continues to move ahead as shown in figure (e).

---

Competition between cutting and bowing :

Lets consider a material A with two different solute volume fraction \( f_1 \) and \( f_2 \), where \( f_1 \) < \( f_2 \) And another material B, with a higher elastic modulus having solute volume fraction \( f_1 \).

• The red line shows the variation of stress required for the dislocation to cut through precipitates and the green line shows the relation between stress required to bow dislocation around precipitate.


• The curve (a) shows the variation of stress and precipitate size for a material A having volume fraction \( f_1 \). And curve (d) shows variation of bowing stress vs precipitate size for the same material having same volume fraction. On combining both curve, it can be obseved that maximum strength is achieved at critical precipitate size of \( r_c1 \)


• On increasing the volume fraction, the cutting stress as well as bowing stress both increases. As shown in curve (a & b) and (c & d).


• If the solute is stiffer then strength of the material will be higher, which can be seen from curve (a) and (c)

From above curve it can be concluded that strength of dispersion hardened material, first increases (when cutting stress is predominant) and then decreases (when bowing is predominant)