Stress Tensor

Stress Tensor is at a point is define as the state of stress at that point inside a material in the deformed state, placement, or configuration. the state of strress shows all different stress developed on 3-perpendicular plane passing through that point.

Consider a single crystal in the form of a cube subjected to a combination of normal stresses (\( \sigma_{xx}, \sigma_{yy}, \sigma_{zz} \)) and shear stresses (\( \tau_{xy},\tau_{yz},\tau_{zx} \)). The coordinate axes are chosen parallel to <100> directions if the crystal system is orthogonal (i.e., cubic, tetragonal, or orthorhombic) or to have a specified orientation with respect to the unit cell if it is not. Then the stress tensor for 3D system is given by -

\[ \sigma_{3D} = \begin{bmatrix} \sigma_{xx} & \tau_{xy} & \tau_{xz} \\ \tau_{yz} & \sigma_{yy} & \tau_{yz}\\ \tau_{zx} & \tau_{zy} & \sigma_{zz} \\ \end{bmatrix} \]

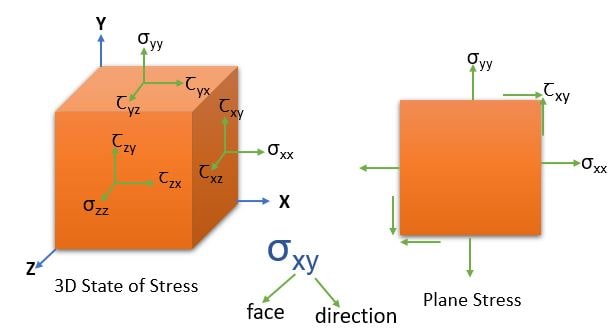
Bi-axial or plane stress :
For plane stress condition any one of the mutually perpendicular faces is assumed to be zero. i.e., \( \sigma_{zz} = \tau_{zx} = \tau_{zy} = 0 \)

\[ \sigma_{2D} = \begin{bmatrix} \sigma_{xx} & \tau_{xy} \\ \tau_{yz} & \sigma_{yy} \\ \end{bmatrix} \]

---

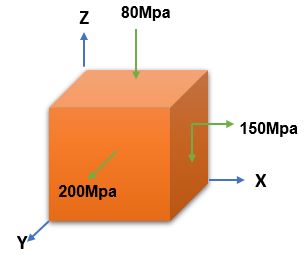Question : Stress analysis of a mechanically loaded structure gives the state of stress as shwn below The stress tensor \( \sigma_{ij} \) of the above structure is given as
\( (A) = \begin{bmatrix} 150 & -30 & 0 \\ -30 & 200 & 0\\ 0 & 0 & -80 \\ \end{bmatrix} \) \( (B) = \begin{bmatrix} 200 & 0 & 0 \\ 0 & 150 & -30\\ 0 & -30 & -80 \\ \end{bmatrix} \) \( (C) = \begin{bmatrix} -80 & 30 & 0 \\ 30 & 150 & 0\\ 0 & 0 & 200 \\ \end{bmatrix} \) \( (D) = \begin{bmatrix} 200 & 0 & 0 \\ 0 & 150 & 0\\ 0 & 30 & -80 \\ \end{bmatrix} \)
Show Answer

---

Strain Tensor

strain tensor at a point is similar to stress tensor at that point but the normal stress is replaced by corresponding normal strain and shear stress by half of the shear strain.
\( \sigma \rightarrow e \)[Normal strain]
\( \tau \rightarrow \frac{\gamma}{2} \)[Shear Strain]

\[ e_{3D} = \begin{bmatrix} e_{xx} & \frac{\gamma_{xy}}{2} & \frac{\gamma_{xz}}{2} \\ \frac{\gamma_{yx}}{2} & e_{yy} & \frac{\gamma_{yz}}{2}\\ \frac{\gamma_{zx}}{2} & \frac{\gamma_{zy}}{2} & e_{zz} \\ \end{bmatrix} \]

\[ e_{2D} = \begin{bmatrix} e_{xx} & \frac{\gamma_{xy}}{2} \\ \frac{\gamma_{yx}}{2} & e_{yy} \\ \end{bmatrix} \]

Question : For given strain tensor below. Find \( \tau_{xy} \) _________ MPa. G= 100GPa

\[ e_{3D} = \begin{bmatrix} 0.002 & 0.004 & 0.006 \\ 0.004 & 0.003 & 0\\ 0.006 & 0 & 0 \\ \end{bmatrix} \]

Show Answer

---

Hydrostatic & Deviatoric Stress

The total stress can be divided into a hydrostatic or mean stress tensor \( \sigma_m \), which involves only pure tension or compression , and a deviator stress tensor \( \sigma^{div}_{ij} \), which represents the shear stresses in the total state of stress. The hydrostatic component of the stress tensor produces only volume change. Such as -
\[ \textrm{Total stress } ( \sigma_{ij} ) = \textrm{Hydrostatic stress } ( \sigma_m ) + \textrm{ Deviator stress } (\sigma^{div}_{ij})\] \[ \sigma_{ij} = \sigma_{ij}^{hydro} + \sigma_{ij}^{div} \]

\[ \begin{bmatrix} \sigma_{11} & \tau_{12} & \tau_{13} \\ \tau_{21} & \sigma_{22} & \tau_{23}\\ \tau_{31} & \tau_{32} & \sigma_{33} \\ \end{bmatrix} = \begin{bmatrix} \sigma_{m} & 0 & 0 \\ 0 & \sigma_{m} & 0\\ 0 & 0 & \sigma_{m} \\ \end{bmatrix} + \begin{bmatrix} \sigma_{11} - \sigma_{m} & \tau_{12} & \tau_{13} \\ \tau_{21} & \sigma_{22} - \sigma_{m} & \tau_{23}\\ \tau_{31} & \tau_{32} & \sigma_{33} - \sigma_{m} \\ \end{bmatrix} \] \[ \textrm{ And, } \sigma_{m} = \frac{\sigma_{11} + \sigma_{22} + \sigma_{33}}{3} \]

Gate 2018 : Consider the following stress state imposed on a material

\[ \sigma_{ij} = \begin{bmatrix} 90 & 50 & 0 \\ 30 & -20 & 0\\ 0 & 0 & 140 \\ \end{bmatrix} \]

If material response elatically with a volumetric strain \( \Delta = 3.5 \times 10^{-4} \), What is its bulk modulus __________ in GPa
Show Answer

Principal Stress and Principal Strain

Complex problems can be solve by considering a simplified two-dimension state of stress. Now consider a stress system which consist of two normal stresses \( \sigma_x \) and \( \sigma_y \) and a shear stress \(\tau_{xy} \). The planes at which the acting shear stresses are zero are known as principal planes and the corresponding stress is known as principal stress.
The above figure shows a thin plate with its thickness is normal to the plane of paper. This stress system consist of two normal stresses \( \sigma_x \) and \( \sigma_y \) and a shear stress \(\tau_{xy} \). In order to know the state of stress from the point O on plane AB we have to resolve the normal and shear stress on the plane AB.