Binary Phase Diagrams

The phase diagrams which based on two components system are called binary phase diagrams

Here, the two compenents can be mixed in a infinite number of different proportions, that is why, composition also becomes a variable apart from pressure and temperature. Depending on the nature (i.e., the crystal structure, the size of atoms, electronegativity, valancy etc.) of these two elements involved, several types of binary equilibria can occure -

(1) Isomorphous Syatem

Isomorphous systems are the simplest form of binary phase diagram. This types of system shows a complete solubility of each other in solid phase as well as in liquid phase. Hence forms a single phase in both solid and liquid phase. These diagrams are called 'isomorphous' because only a single type of crystal structure is obtained at the all possible compositions.
Examples : Cu-Ni, Au-Ag, Au-Cu, Mo-W, Mo-Ti etc.

The above figure shows the classic example of isomorphous system of Cu - Zn alloy. Pure copper (FCC) melts at 1083^oC whereas pure nickel (FCC) melts at 1455^oC. Here, the liquid solution which is a single phase extended over all composition. Similarly the single phase solid solution (\( \alpha \)), forms over entire range of composition. These solid and liquid phases are seperated be a two phase region, where both the phases (\( \alpha + L \)) are stable. In two phase region, complete solidification does not occure at a single point instead solidification occures over a range of temperature.

The tie - line rule : Prediction of chemical composition of phases

In a single phase region, it is quite straight forward to determine the chemical composition of that phase at a given temperature. For example, at 900^oC and 50 wt.% Ni, the \( \alpha \) phase have 50 Cu and 50 Ni (wt. %). But things get complicated when we move to two phase region ( \( \alpha + L \) ). At 1300^oC and 50 wt.% Ni, we can not directly determine the composition of liquid phase (L) and, composition of solid phase (\( \alpha \)). So here we draw a line parallel to composition axis at the desired temperature known as the tie line and, the intersection points of tie line with liquidus and solidus line will give use the chemical composition of the respective phases.

As in the above Cu-Ni phase diagram, a tie line (green color) is drawn at the temperature of 1300^oC. The tie line cuts liquidus at C_L point and solidus at C_S. Hence, for an Cu alloy containing 50 wt.% Ni at 1300^oC will have two phases \( \alpha \textrm{ and } L\). Furthermore, the \( \alpha \) phase will have Ni composition of C_S wt%, and the liquid phase will have Ni composition of C_L wt%.

The lever rule : Prediction of amount of phases

The relative amount of phases present in a two phase region at a specific temperature can be determined by the lever rule. The lever rule obtained from two principles -

• Conservation of mass, let \( W_s \) and \( W_l \) be the weight frations of solid and liquid in two phase rigion then sum of fractional amounts must be unity. \[ W_s + W_l = 1 \]
• The mass of solute B distributed between two phases (i.e., solid and liquid) must be equal to the mass of solute present in the overall alloy \[ W_s C_s + W_lC_l = C_0 \]

The fractional amount of solid (\( W_s \)) and liquid (\( W_l \)) in the alloy given by

\[ \boxed{ W_s = \frac{C_0 - C_l}{C_s - C_l} = \frac{a}{L} } \] \[ \boxed{ W_l = \frac{C_s - C_0}{C_s - C_l} = \frac{b}{L} } \]

The above diagram shows a part of Cu-Ni phase diagram. Here, applying the lever rule to know the amount of phases present in the alloy (27 Ni, 73 Cu) at 1200^oC.

• First we draw a horizontal line (tie-line) thruogh point 'O' for the given temperature (1200^oC)
• From intersection points of tie line on two phase region, composition of solid and liquid in the alloy is determined. Composition of \( C_L = 22\% \) and composition of solid \( C_S = 38\% \)
• Form a lever from intersection points (i.e., \( C_l \) and \( C_s \)) and O.
• \( C_L \) and \( C_S \) becomes the two ends of lever having the fulcrum at the point O. a and b are the arms of the lever, such that a + b = L

Fraction of solid in alloy (27 Ni, 73 Cu) at 1200^oC \[ \displaylines{ W_s = \frac{C_0 - C_l}{C_s - C_l} \\ = \frac{a}{L} \\ = \frac{5}{16} \\ = 0.3125\% } \] Fraction of liquid in alloy (27 Ni, 73 Cu) at 1200^oC \[ \displaylines{ W_l = \frac{C_s - C_0}{C_s - C_l} \\ = \frac{b}{L} \\ = \frac{11}{16} \\ = 0.6875\% } \]

---

(2) Type-I : Eutectic System (Completely insoluble in solid state)

In this type of alloy system, the two components are completely soluble in liquid state but completely insoluble in each other in solid phase. As there are only few numbers of alloy system which can satisfy one, or more Hume Rothery rules, therefore such type of alloy system doesn't show substitutional solid solubility.
Examples : Pb-As, Bi-Cd, Au-Si

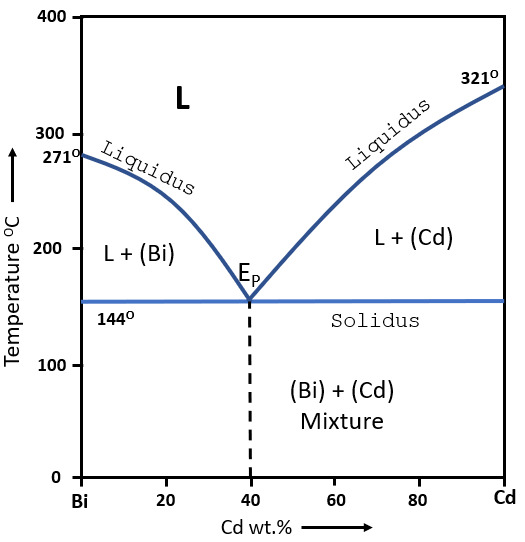
The above figure shows a eutectic phase diagram of Bi - Cd alloy. The elements of alloy are completely insoluble in each other in solid state. At all the composition, the solidification occures over a range except a certain composition which shows solidifiaction at a fixed temperature of 144^oC. The alloy (60% Bi, 40% Cd) called eutectic alloy which shows a solidification at a single temperature of 144^oC. The eutectic reaction is given as -

\[ L \textrm{ (60% Bi, 40% Cd) } \longrightarrow \textrm{ Pure Bi } + \textrm{Pure Cd} \]

---

(3) Type-II : Eutectic System (Partial soluble in solid state)

In this type of alloy system, the two components are completely soluble in liquid state, and partial soluble in solid phase. Since most of the metal show limited solid solubility in each other, so these type of phase diagram become most common and important.
Examples : Pb-Sn, Cu-Ag, Pb-Sb, Cd-Zn, Sn-Bi

The above figure shows a eutectic phase diagram of Pb - Sn alloy. The solid phase at the left-end of phase diagram is a Pb-rich \( \alpha \) phase, which is the solid solution of Sn in Pb. \( \alpha \) dissolves only a limited amount of tin. In the same way, the solid phase at the right-end is a Sn-rich \( \beta \) phase, which is the solid solution of Pb in Sn. These two solid solution at the end is known as terminal solid solution.
The above Pb-Sn diagram, the \( \alpha \textrm{ and } \beta \) have terminal solid solubility of 19% and 97.5% respectivity. The liquidus line shows a minima at point 'E_P', where solidus and liquidus line merage and become a single point, which is known as eutectic point and at this point, liquid solidify at a single temperature. At the eutectic temperature, the following eutectic reaction occures as -

Microstructural changes during cooling of eutectic alloy

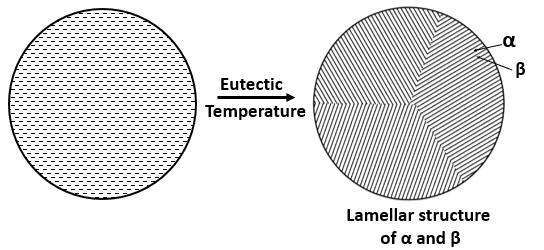
On cooling an eutectic alloy, the solid product will be the mixture of two solution, \( \alpha \textrm{ and } \beta \) and, will form a inter-lamellar structure which have thin and, parallel plates of alternate \( \alpha \) and \( \beta \) crystals. The fraction of \( \alpha \textrm{ and } \beta \) phase in the mixture can be determine by using the lever rule.
\[ \alpha \textrm{ phase wt.% in eutectic mixture} = \frac{97.5 - 61.9}{97.5 - 19} \times 100 = 45.35\% \] \[ \beta \textrm{ phase wt.% in eutectic mixture } = \frac{61.9 - 19 }{97.5 - 19} \times 100 = 54.65\% \]

Microstructural changes during cooling of hyper-eutectic (above eutectic composition ) alloy
On cooling a hypereutectic alloy (20%Pb, 80%Sn) under equlibrium conditions. temperature is aabove the liquidus then it will form a single liquid phase as shown in figure (a). At a temperature below liquidus, solidification starts with a formationof a very small solid phase knowns as PRO-eutectic \( \beta \) (because this solid phase is forming before the eutectic temperature). At a lower temperature T₁, the amount of \( \text{proeutectic } \beta \) phase will increase. Its composition is now different and can be determined by drawing a tie-line at the T₁ temperature as shown by the green line in the phase diagram. The microstructure at temperature T₁ will look like as shown in figure (b).

Just above eutectic temperature, the quantity of proeutectic \( \beta \) will be at its max. and the overall proeutectic - \( \beta \) phase can be obtained by drawing tie-line at eutectic temperature.
On futher cooling to just below the eutectic temperature, the remaining liquid will transform according to eutectic reaction (i.e, form lamellar structure) as discussed above. The final microstructure as shown in figure (c), will contain large equiaxed (or same size) crystal of proeutectic \( \beta \), that is, \( \beta \) formed just before the eutectic temperature or eutectic reaction, and the matrix will be eutectic mixute consisting of thin and, parallel plates of alternate \( \alpha \) and \( \beta \) crystals.

---

(4) Eutectoid System

Similar to eutectic inverient reaction, this type of inverient reaction occures entirely in the solid state, where a single solid phase gets transform to mixture of two solid phase.
Example : Ag-Cd, Al-Mn, Au-Zn, Cu-Zn, Cu-Sn, Cu-Si
The eutectoid reaction is given by -

\[ \gamma \textrm{ (solid, A) } \longrightarrow \alpha \textrm{ (solid, B) } + \beta\textrm{ (solid, C)} \]

---

(5) Peritectic System

When the melting points of the components are differ vastly from each other than a peritectic phase diagram may form. In this type of syatem, a two phase mixture of a liquid and a solid transform to a single phase solid.
Example : Ag-Pt
The peritectic reaction is given by -

\[ L \textrm{ (liquid) } + \beta\textrm{ (solid, A)} \longrightarrow \alpha \textrm{ (solid, B) } \]

---

Summary of the invariant reactions

#	Name	Invarient raction
1	Eutectic	\( L \longrightarrow \alpha + \beta \)
2	Eutectoid	\( \gamma \longrightarrow \alpha + \beta \)
3	Monotectic	\( L_1 \longrightarrow L_2 + \alpha \)
4	Peritectic	\( L + \alpha \longrightarrow \beta \)
5	Peritectoid	\( \gamma + \alpha \longrightarrow \beta \)
6	Syntectic	\( L_1 + L_2 \longrightarrow \alpha \)