Crystal Structure of Solids

Crystal, any solid material in which array of atoms of solid are arranged in a orderly and periodic pattern and whose surface regularity reflects its internal symmetry.

Crystalline Vs Amorphous solids :
Crystalline are those material which exhibits 3D long range periodicity of arrangement of atom or molecules or ions. Crystallinity can be seen in metals, many ceramics and some polymer.
Amorphous have no periodic packing of atoms or molecules or ions. Occures from rapid cooling.

CRYSTALLINE SOLIDS	AMORPHOUS SOLIDS
Sharp melting point	No particular melting point
Anisotropic	Isotropic
True solid	Pseudo solid
Symmetrical	Unsymmetrical
More rigid	Less rigid
Long range order	Short range order
Example: Potassium nitrate, copper	Example: Fibre Glass, PVC, Teflon etc.

What is Lattice :
➧ A lattice is an infinite array of points
➧ Lattice is a translationally periodic arrangement of points
➧ Each lattice point is identical to every other point, i.e., the environment around one lattice site is identical to that around every other.
➧ Each point in the lattice is defined by \( R = n_{1}a_{1} + n_{2}a_{2} + n_{3}a_{3} \)

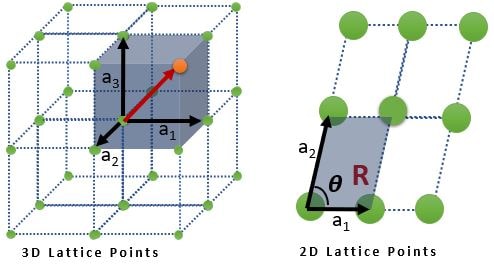
where \( n_{1} , n_{2} \textrm{ and } n_{3} \) is a set of three integers and \( a_{1} , a_{2} \textrm{ and } a_{3} \) are (known as the primitive vectors) three non coplanar vectors.

Unit Cell :
From Above figure, any parallelogram (and parallelopiped in 3D), connecting all lattice points is called a unit cell. There are infinite possibilities for unit cells.
In simple words The smallest repeating unit of the crystal lattice is the unit cell, and it should refect crystal's symmetry.

Types of Unit cell :
• Primitive Unit cell : Unit cell having one formula unit or one lattice point
• Non-primitive Unit cell : Unit Cell having more than one formula units or lattice points


Crystal Structure :
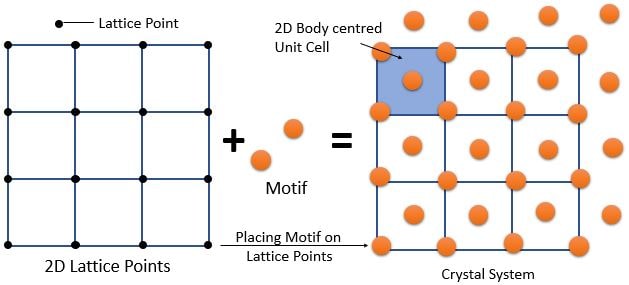
➧ Crystal structure can be constructed in many ways. Example : A Lattice and Motif (i.e., atom of group of atoms).
➧ There are many combinations of lattices and motifs possible that can result in the same crystal. There is no unique choice. \[ \textrm{ Crystal Structure = Lattice + Motif } \]

Crystal System

Based on XRD technique, all crystalline materials are classified into 7-crystal system. And these 7-crystal system further divided into 14 Bravais lattices .

Crystal System	Geometry	Crystal Symmetry	Bravais Lattices
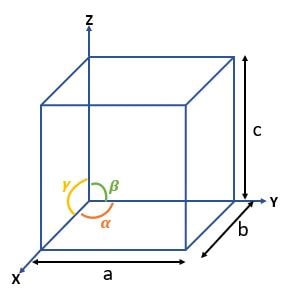
Cube	\( a = b = c \textrm{ ; } \alpha = \beta = \gamma = 90^\circ \)	4 , 3-fold rotation axes	3 → SC, BCC, FCC
Tetragonal	\( a = b \neq c \textrm{ ; } \alpha = \beta = \gamma = 90^\circ \)	1 , 4-fold rotation axes	2 → ST, BCT
Orthorhombic	\( a \neq b \neq c \textrm{ ; } \alpha = \beta = \gamma = 90^\circ \)	3 , \( \perp \) 2-fold rotation axes	4 → SO, BCO, FCO, ECO
Rhombohedral	\( a = b = c \textrm{ ; } \alpha = \beta = \gamma \neq 90^\circ \)	1 , 3-fold axis symmetry	1 → SR
Hexagonal	\( a = b \neq c \textrm{ ; } \alpha = \beta = 90^\circ \textrm{ ; } \gamma = 120^\circ \)	1 , 6-fold rotation axes	2 → SH
Monoclinic	\( a \neq b \neq c \textrm{ ; } \alpha = \beta = 90^\circ \neq \gamma \)	1 , 2-fold rotation axes	2 → SM, ECM
Triclinic	J\( a \neq b \neq c \textrm{ ; } \alpha \neq \beta \neq \gamma \neq 90^\circ \)	None	1 → S.Triclinic
		Total Bravais Lattices :	14

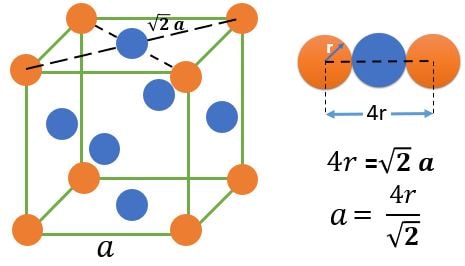
FCC (Face Centered Cubic) :
Atom Positions :
    (1) 8 Atoms, At every corner contributing \( \frac{1}{8} \) => 8 Corner atoms \( \times \) \( \frac{1}{8} \) contribution = 1 atom
    (2) 6 Atoms, At every face center contributing \( \frac{1}{2} \) => 6 Face centered atoms \( \times \) \( \frac{1}{2} \) contribution = 3 atom
    Total number of atoms = 1+3 = 4 atoms.


Notes :
    (1) FCC Elements are generally strong and ductile
    (2) Examples :- \( \gamma-Fe \), Al, Cu, Ni, Au, Ag, Pt.


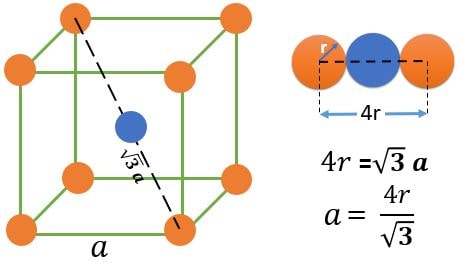
BCC (Base Centered Cubic) :
Atom Positions :
    (1) 8 Atoms, At every corner contributing \( \frac{1}{8} \) => 8 Corner atoms \( \times \) \( \frac{1}{8} \) contribution = 1 atom
    (2) 1 Atoms, At every Body center contributing 1 => 1 atom
    Total number of atoms = 1+1 = 2 atoms.


Notes :
    (1) BCC Elements are generally hard and brittle
    (2) Examples :- \( \alpha-Fe \), \( \delta-Fe \), W, Cr, V, Mo, Ta.


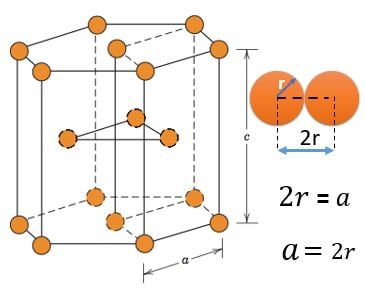
HCP (Hexagonal Closest Packed) :
Atom Positions :
    (1) 12 Atoms, At every corner contributing \( \frac{1}{6} \) => 12 Corner atoms \( \times \) \( \frac{1}{6} \) contribution = 2 atom
    (2) 2 Atoms, At top and bottom face center contributing \( \frac{1}{2} \) => 2 Face centered atoms \( \times \) \( \frac{1}{2} \) contribution = 1 atom
    (3) 3 Atoms, Inside HCP structure contributing 1 => 3 atom
    Total number of atoms = 2 + 1 + 3 = 6 atoms or 2 Atom per Unit (1HCP has 3 Unit structures )


Notes :
    (1) HCP Elements are generally less ductile compare to FCC
    (2) For regular HCP Element \( \frac{c}{a} = \sqrt{\frac{8}{3}} = 1.632 \).
    (3) Examples :- Mg, Zn, Zr, Ti, Co.


Coordination Number :
CN is define as the total number of nearest and equi-distance atoms surrounding an atom under consideration.

	SC	FCC	BCC	HCP	DC
CN	6	12	8	12	4

Atomic Packing Factor :
APF is define as the ratio of total avg. volume( Number of atoms \(\times \) total number of atom ) occupied by atoms to the volume of the unit cell.

\[ APF = \frac{N_{atoms} \times V_{atoms}}{V_{\textrm{unit cell}}} = \frac{N \times \frac{4}{3} \pi r^3}{a^3} \]

	SC	FCC	BCC	HCP	DC
APF	0.52	0.72	0.68	0.72	0.34

---

Density Calculation for Crystal Structures

Generally, 3 type of densities are calculated in a crystal structure.

Volume Density or Theoratical Density or X-Ray Density :

\[ \rho_{v} = \frac{\textrm{Wt. of avg. no of atoms}}{\textrm{Volume of unit cell}} = \frac{Z \times M_{w}}{N_{A} \times a^3} \]

unit : \( \frac{g}{m^3} \)
Where ,
       Z = Number of atoms in unit cell (atoms)
       \(M_{w} = \) Molar Mass (g/mol)
       \(N_{A} = \) Avogadro’s number = \( 6.023 \times 10^{23} \) \( \frac{atom}{mol} \)
       V = Volume of unit cell = \( a^3 \) \( ( m^3 ) \)

Planer Density :
Planer Density is define as the Ratio of number of atoms who's centers are intersected by the plane to the area of the plane itself.

\[ \rho_{PL} = \frac{\textrm{Number of atomes in that plane}}{\textrm{Area of plane}} \]

unit : \( \frac{atoms}{m^2} \)

Plane	FCC	BCC
(100)	\[ \frac{2}{a^2} \]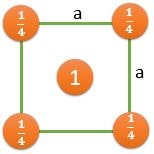	\[ \frac{1}{a^2} \]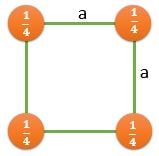
(110)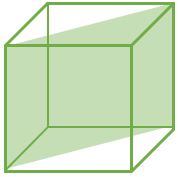	\[ \frac{2}{\sqrt{2}a^2} \]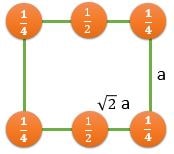	\[ \frac{2}{\sqrt{2}a^2} \textrm{ } (CPP) \]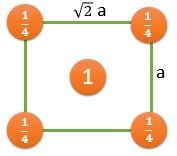
(111)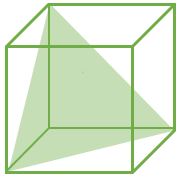	\[ \frac{2}{(\sqrt{3}/2)a^2} \textrm{ } (CPP) \]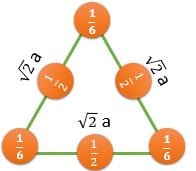	\[ \frac{1/2}{(\sqrt{3}/2)a^2} \]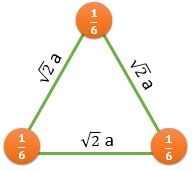

CPP (Closest Packed Plane): These planes have higher value of planer density. Hence, Slip occurs in such planes
       For FCC : (111) Plane
       For BCC : (110) Plane

Linear Density :
Linear density defined as the number of atoms whose centers are intersected by a line to the length of the line itself.

\[ \rho_{l} = \frac{\textrm{Number of atomes intersected by line}}{\textrm{Length of direction vector i.e, line}} \]

unit : \( \frac{atoms}{m} \)

Direction	FCC	BCC
[100]	\[ \frac{1}{a} \]	\[ \frac{1}{a} \]
[110]	\[ \frac{2}{\sqrt{2}a} \textrm{ } (CPD) \]	\[ \frac{1}{\sqrt{2}a} \]
(111)	\[ \frac{1}{(\sqrt{3})a} \]	\[ \frac{2}{(\sqrt{3})a} \textrm{ } (CPD)\]

CPD (Closest Packed Direction): These Directions have higher value of Linear density. Hence, Slip occurs in such direction
       For FCC : [110] Direction
       For BCC : [111] Direction