Third Law of Thermodynamics

Nernst stated that the entropy change for each chemical or physical transition between condensed phases, at temperatures very close to the absolute zero, is equal to zero. \[ \lim_{T\to 0} \Delta S = 0 \] This statement is also referred to as the Nernst heat theorem. The statement of Nernst was simplified by Planck. He stated that not only the entropy change for processes but also the actual entropy of each condensed substance equals zero if the temperature approaches absolute zero.

3rd LoT states that, when the temperature of a pure crystalline substance approaches absolute 0K, its entropy approaches zero. \[ \boxed{ T \rightarrow 0 \Rightarrow S \rightarrow 0 } \]

Alternate Statement of 3rd LoT

It states that, it is imposible to reduce a body temperature to 0K in a finite number of steps no matter how idealize each step is followed. The figure below shows that how many finite adiabatic/isothermal process you take you will not be able to reach absolute zero temperature.

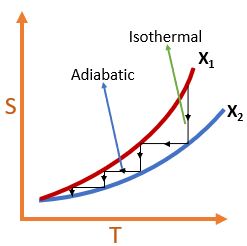
Application of 3rd LoT

Calculating transformation entropy of elements.
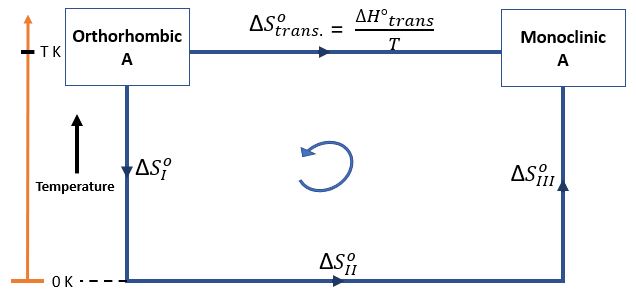
Let's consider an example, pure orthorhombic A transform to stable monoclinic A at a temperature T K. \[ \textrm{As we know, } \Delta S^{0}_{Cycle} = 0 \] \[ \Rightarrow \Delta S^{0}_{I} + \Delta S^{0}_{II} + \Delta S^{0}_{III} - \Delta S^{0}_{trans} = 0 \] \[ \Rightarrow \Delta S^{0}_{trans} = \Delta S^{0}_{I} + \Delta S^{0}_{II} + \Delta S^{0}_{III} \] \[ \textrm{And as entropy change = 0 at T=0 K , } \Rightarrow \Delta S^{0}_{II} = 0 \]

\[ \Rightarrow \boxed{ \Delta S^{0}_{trans} = \Delta S^{0}_{I} + \Delta S^{0}_{III} } \]

Question :A pure monoclinic sulpher transform to rhombodedral sulpher at 400K. By application of third law , the value of entropy change for this transformation is __________________ \( JK^{-1} \) ?
Given \( S^{0}_{\textrm{monoclinic S, 0 }\rightarrow 400K} = 36.2 JK^{-1}\)
And, \( S^{0}_{\textrm{rhombodedral S, 0 }\rightarrow 400K}= 38.6 JK^{-1}\)

Show Answer

Gibbs Free Energy (G)

Gibbs free energy is defined as the total energy available to do thermodynamic work (non-PV) in a closed system at constant pressure and temperature. \[ G = \underbrace{ U + PV}_\text{H} - TS \] \[ \boxed{G = H - TS } \]

Helmholts Free Energy (F)

The Helmholtz free energy is a thermodynamical potential that measures the maximum amount of "useful" (non-PV) work that can be obtained from a closed system at constant volume and temperature. \[ \boxed{F = U - TS } \]

Maxwell Relations

Important Formula's
1) If \( z = f(x,y) \)

\( dz = \Big(\frac{\partial z}{\partial x}\Big)_{y}dx + \Big(\frac{\partial z}{\partial y}\Big)_{x}dy \) \( \Rightarrow dz = Mdx + Ndy \)

So, If z is an exact differential \[ \Bigg(\frac{\partial M}{\partial y}\Bigg)_{x} = \Bigg(\frac{\partial N}{\partial x}\Bigg)_{y} \] 2) If \( z = f(x,y) \) \[ \Bigg(\frac{\partial z}{\partial x}\Bigg)_{y} . \Bigg(\frac{\partial x}{\partial y}\Bigg)_{z} . \Bigg(\frac{\partial y}{\partial z}\Bigg)_{x} = -1 \]

---

Thermodynamics Maxwell Relations

These relations derivable from the symmetry of second derivatives of thermodynamics functions and from the definitions of the thermodynamic potentials. And these thrmodymics equations help in finding relation between various thermodynamic quantities (e.g., pressure P, volume V, temperature T and Entropy S) in thermodynamic equilibrium.

1) From TDS => TdS = dU + PdV
=> dU = TdS - PdV

\[ \Bigg(\frac{\partial T}{\partial V}\Bigg)_{S} = - \Bigg(\frac{\partial P}{\partial S}\Bigg)_{V} \]

2) From TDS => TdS = dH - VdP
=> dH = TdS + VdP

\[ \Bigg(\frac{\partial T}{\partial P}\Bigg)_{S} = \Bigg(\frac{\partial V}{\partial S}\Bigg)_{P} \]

3) G = H - TS
=> dG = dH - TdS - SdT = VdP - SdT

\[ \Bigg(\frac{\partial V}{\partial T}\Bigg)_{P} = - \Bigg(\frac{\partial S}{\partial P}\Bigg)_{T} \]

4) F = U - TS
=> dF = dU - TdS - SdT = -PdV - SdT

\[ \Bigg(\frac{\partial P}{\partial T}\Bigg)_{V} = \Bigg(\frac{\partial S}{\partial V}\Bigg)_{T} \]