Second law of thermodynamics and Concept of Entropy

The second law of thermodynamics states that for any spontaneously occurring process the entropy (S) of the universe will always increase. Isolated systems spontaneously evolve towards the thermal equilibrium which is the state of maximum entropy of the system . In simple words, this law explains that the for an isolated system the entropy will never decrease over time.

For more understanding, let us consider a person's room that is not cleaned and tidied. Regardless of how much effort he put to keep it clean, it will invariably become more messy and disorderly with time. And if he put action to clean the room, its entropy decreases, but the action to clean it has resulted in increasing entropy outside (surrounding) the room that exceeds the lost entropy. Which can be concludes as : -

\[ \boxed{ S_{Total} = S_{surroundings} + S_{System} > 0 } \]

Different Statements of The Law

There are two statements on the second law of thermodynamics which are:
            (1) Kelvin- Plank Statement
            (2) Clausius Statement

Kelvin- Plank Statement :

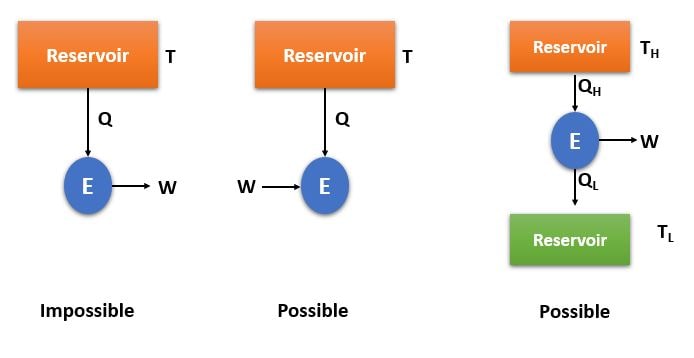
This statement says that , it is imposible to develop a heat engine/device operating on a cycle that produces work by exchanging heat with single reservoir.

\[ \eta = \frac{W}{Q} = \frac{Q_{L} - Q_{H}}{Q_{L}} \] \[ \eta = 1 - \frac{Q_{L}}{Q_{H}} \] Clausius Statement :

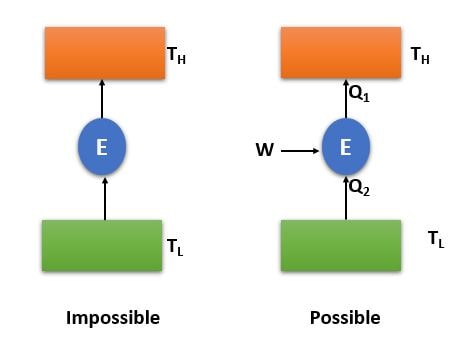
This statement says that , it is imposible to develop a heat engine/device operating on a cycle which can tranfer heat from a body of lower temperatute to a body of higher temperature without any energy input.

Entropy (S)

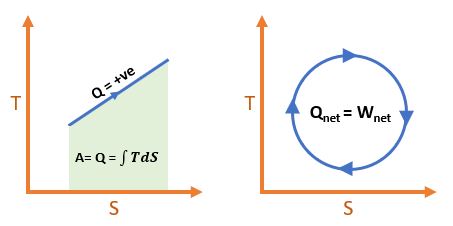
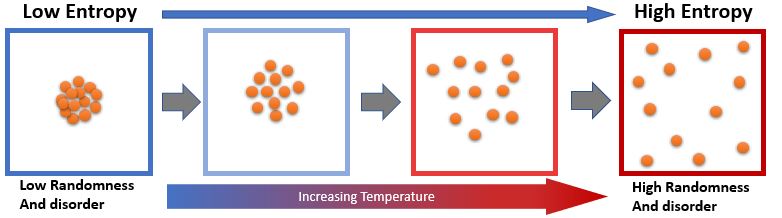
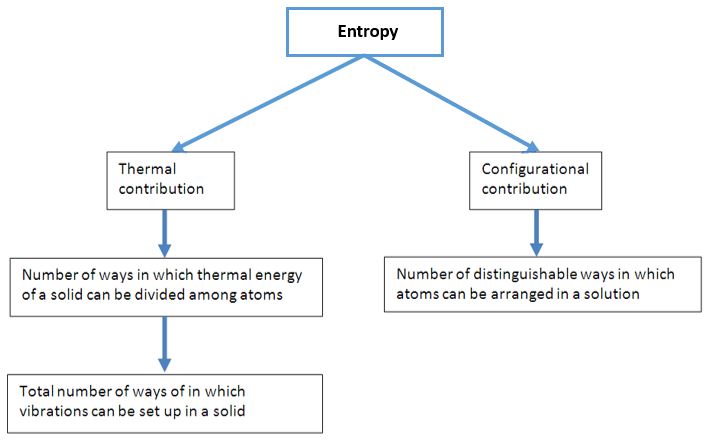
Entropy can be defined as a measure of randomness or molecular disorder disorder of a system. Spontaneous processes in isolated systems occur only if it is accompanied by an increase in entropy. Entropy helps in determining the free energy available to do work. Entropy Is an State function.
Unit : \( J.Kg^{-1}.K^{-1} \)

Question :The entropy of an isolated system can never _______?

a) increase
b) decrease
c) be zero
d) none of the mentioned
Show Answer

Components of Entropy :

Entropy Change :

The change in entropy of the surroundings is essentially just a measure of how much energy is being taken in from surrounding or given off by the system to surrounding. Under isothermal conditions, we can express the entropy change of the surroundings as: \[ \frac{\delta Q}{T} + \delta \hat{S}_{gen} = dS \] Where \( \delta \hat{S}_{gen} \) is Entropy genetrated during any process.

For Irreversible Process :
A irreversible process, which involves the spontaneous movement of a system from a non-equilibrium state to an enquilibrium state can be defined as spontaneous or natural process.And such processes cannot be reversed without help of any external agency, thus it is called an irreversible process. Here \( \delta \hat{S}_{gen} > 0 \) means possible process. \[ \boxed{ \Rightarrow \frac{ \delta Q}{T} < dS } \]

For Reversible Process :
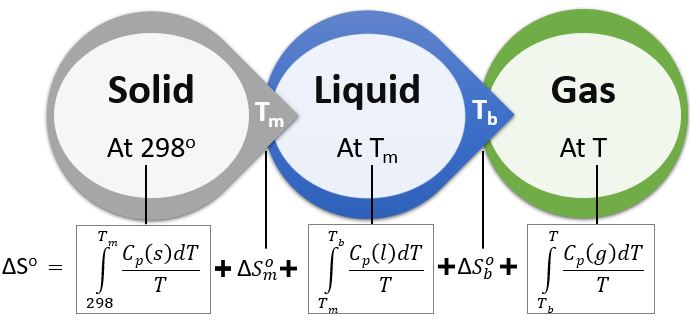
A reversible process, which takes a system from a state A to another state B is one in which the process path passes through a continuum of equilibrium states. Thus a reversible process is the one during which the system never away from the equilibrium . Which indicate \( \delta \hat{S}_{gen} = 0 \) \[ \Rightarrow \frac{ \delta Q}{T} = dS \] \[ \textrm{On Integration } \Delta S = \int_{T_{i}}^{T_{f}} mC_{p}\frac{dT}{T} \] \[ \boxed{ \Rightarrow \Delta S = mC_{p}\ln{\frac{T_{f}}{T_{i}}} } \]

For Reversible Adiabatic Process :
As for such processes \( dQ = 0 \) \[ \boxed{ \Rightarrow dS = 0 } \]

---

TDS Equations

(i) 1st TDS Equation
As from First Law : \[ dU = \delta Q - \delta W \] \[ \Rightarrow \delta Q = dU + PdV \] \[ \textrm{As } \delta Q = TdS \Rightarrow \boxed{TdS = dU + PdV} \] (ii) 2nd TDS Equation
As from enthalpy equation : \[ H = U + PV \] \[ \Rightarrow dH = dU + PdV + VdP \] \[ \textrm{As } TdS = dU + PdV \Rightarrow dH = TdS + VdP \] \[ \Rightarrow \boxed{TdS = dH - VdP} \]

Important Equations to calculate Entropy Change (For Ideal Gas)

\( \textrm{(1) } \Delta S = C_{V}\ln{\frac{T_{2}}{T_{1}}} + R\ln{\frac{V_{2}}{V_{1}}} \)

\( \textrm{(2) } \Delta S = C_{P}\ln{\frac{T_{2}}{T_{1}}} - R\ln{\frac{P_{2}}{P_{1}}} \)

\( \textrm{(3) } \Delta S = C_{V}\ln{\frac{P_{2}}{P_{1}}} + R\ln{\frac{V_{2}}{V_{1}}} \)

Finite Body Analysis

Let's consider two Incompressible fluids or Solid bodies having (Mass \(m_{1}\), Specific Heat \(C_{1}\), Temparature \(T_{1}\) ) and (Mass \(m_{2}\), Specific Heat \(C_{2}\), Temparature \(T_{2}\) ) respectively, are brought in contact with each other to attain a common equilibrium temperature.

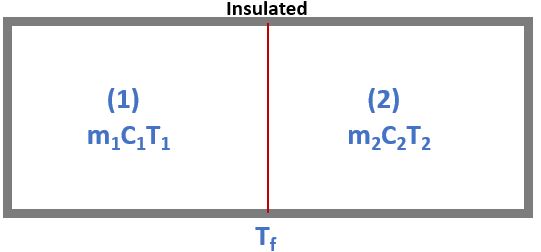
According to first law
\( dU = \delta Q - \delta W \) and Also here, \(\delta Q =0 \textrm{ and } \delta W = 0 \Rightarrow dU = 0 \)
\[ \Rightarrow (dU)_{1} + (dU)_{2} = 0 \] \[ \Rightarrow m_{1}C_{1}(T_{f} - (T_{1}) = m_{1}C_{1}(T_{f} - (T_{2}) \] \[ \boxed{ T_{f} = \frac{ m_{1}C_{1}T_{1} + m_{2}C_{2}T_{2}}{m_{1}C_{1} + m_{2}C_{2}} } \] Entropy change
\( (\Delta S)_{Universe} = (\Delta S)_{System} + (\Delta S)_{Surrounding} \)

As, For Insulated System, \( (\Delta S)_{Surrounding} = 0 \)
\( \Rightarrow (\Delta S)_{Universe} = (\Delta S)_{1} +(\Delta S)_{2} \)
\( \Rightarrow (\Delta S)_{Universe} = m_{1}C_{1}\ln{\frac{T_{f}}{T_{1}}} + m_{2}C_{2}\ln{\frac{T_{f}}{T_{2}}} \)

Now If Assuming , \( m_{1} = m_{2} \textrm{ and } C_{1} = C_{2} \)
\( \Rightarrow (\Delta S)_{Universe} = mC\ln{\frac{T_{f}}{T_{1}}} + mC\ln{\frac{T_{f}}{T_{2}}} \)
\( \Rightarrow (\Delta S)_{Universe} = mC\ln{\frac{T_{f}^2}{T_{1}T_{2}}} = 2mC\ln{\frac{T_{f}}{\sqrt{T_{1}T_{2}}}} \)
\[ \Rightarrow \boxed{ (\Delta S)_{Universe} = 2mC\ln{\frac{AM}{GM}}} \] \[ \textrm{For N bodies } \boxed{ (\Delta S)_{Universe} = NmC\ln{\frac{AM}{GM}} } \]

Question :An 1 Kg of Steel iron at 800K brought in contact with another 1Kg of Iron at 600K and both allow to thermal equilibrium. Find Equilibrium temperature _____K and Entropy change for this process_________\( JK^{-1} \)
Given C = 0.462 \( Jg^{-1}K^{-1} \)
Assume Isolated System.

Show Answer

---

Important Note :
For any Cyclic Process , All path function parameter will be equal to 0.

1) \( (\Delta S)_{Cycle} = 0 \)
2) \( (\Delta U)_{Cycle} = 0 \)
3) \( (\Delta H)_{Cycle} = 0 \)

T-S Diagram

1. For any reversible Process Area 'A' under T-S diagram gives net Heat transfer(Q) for the process
2. Every process from left to right is taken +ve
3. For any cyclic process the Area enclosed by the cycle on T-S diagram gives net Heat transfer
4. As For cyclic Process \( dU = 0 \), Means \(Area = Q_{net} = W_{net} \)

Entropy change for pure substance

Pure substance , every reversible process of phase change at a constant pressure occures at a constant temperature. So for such conditions \( \delta Q = \delta H \). \[ \Delta S^{o} = \frac{\Delta H_{transformation}}{T_{transformation}} \] Lets calculate Entropy change for a pure subtance where phase changes from solid to Gas.