 Learn Metallurgy
Learn Metallurgymail@learnmetallurgy.com
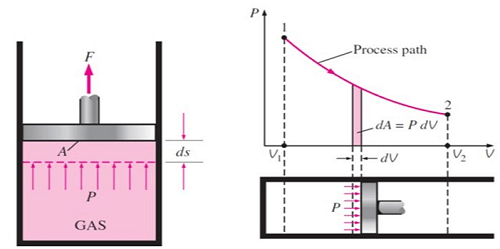
In thermodynamics, work performed by a system is the energy transferred by the system to its surroundings and for a closed system it is equal to area under P-V diagram when projected on the volume axis as shown below.
$$\delta W = P \partial V$$
$$ \boxed{ W = \int_{1}^{2} P dV }$$
As \( PV^ \gamma = C \)
\[ \textrm{ Now, } P \left( \frac{T}{P} \right)^\gamma = C
=> \frac{T_{2}}{T_{1}} = \left({ \frac{P_{2}}{P_{1}} } \right)^{\frac{\gamma - 1 }{ \gamma }}
\textrm{ Also, } \frac{T_{2}}{T_{1}} = \left({ \frac{V_{1}}{V_{2}} } \right)^{\gamma - 1 } \]
As \( PV^n = C \)
\[ \textrm{ Now, } \frac{T_{2}}{T_{1}} = \left({ \frac{P_{2}}{P_{1}} } \right)^{\frac{n - 1 }{ n }}
\textrm{ Also, } \frac{T_{2}}{T_{1}} = \left({ \frac{V_{1}}{V_{2}} } \right)^{n - 1 } \]
Answer : W = 5762.82J
As for Isothermal process \( W = C \ln{\frac{V_{2}}{V_{1}}} \)
As given \( V_{f} = 2V_{i} \) , Mole n = 1, T = 1000K And R=8.324 J/mol-K
=> \( W = nRT \ln \frac{V_{2}}{V_{1}} \)
=> \( W = 1 \times 8.314 \times 1000 \ln \frac{V_{2}}{V_{1}} = 1 \times 8.314 \times 1000 \ln{2} \)
=> \( W = 5762.82J \)
| K | Process | Expansion | Compression |
|---|---|---|---|
| 0 | P=C Isobaric | 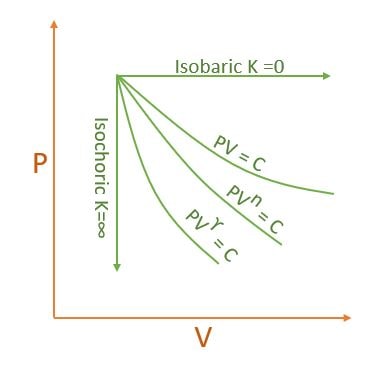 |
 |
| \( \infty \) | V=C Isochoric | ||
| 1 | T=C Isothermal | ||
| \( \gamma \) | Adiabatic | ||
| n | Polytropic |
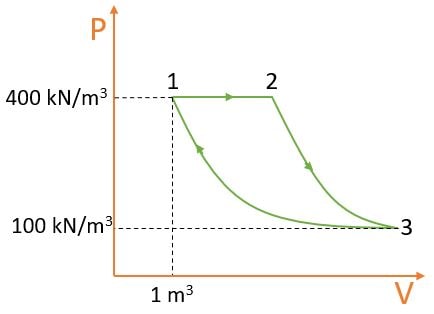
As 3 - 1 Isothermal Process i.e., PV = C => \( P_{1}V_{1} = P_{3}V_{3} \)
\( => 400 \times 1 = 100 \times V_{3}\)
\( V_{3} = 4 m^3 \)
For 2 - 3 Polytropic Process i.e., \( PV^n = C => P_{3}V_{3}^n = P_{2}V_{2}^n \)
\( => 100 \times 4^1.4 = 400 \times V_{2}^n \)
\( V_{2} = 1.43 m^3 \)
Wnet = \( W_{1-2} + W_{2-3} + W_{3-1}\)
Wnet = \( P_{2}(V_{3} - V_{1}) + \frac{ P_{2}V_{2} - P_{3}V_{3} }{ n - 1} + C \ln{\frac{V_{3}}{V_{1}}} \)
Wnet = \( 192.00 + 480 - P_{3}V_{3} \ln{\frac{V_{3}}{V_{1}}} \)
Wnet = 125.88KJ
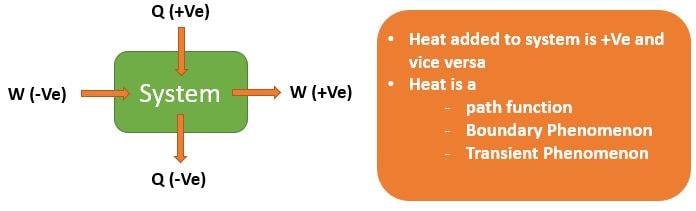
Heat is the form of energy generated due to difference in the temperature difference between substances or systems. As a form of energy, heat is conserved, i.e., it cannot be created or destroyed.
Heat is directly proportional to mass(m) i.e., Q ∝ m
Also, Heat generated in the presence of thermal gradient(ΔT) i.e., Q ∝ ΔT
\[ \boxed{ \delta Q = mCdT } \]
Where , C = Specific Heat Capacity \( \frac{kJ}{kg-K} \textrm{ or } \frac{kJ}{mol-K} \)
Specific Heat Capacity(C) :
It is the amount of energy of energy required to change the temperature of unit mass of a substance through unit degree temperature difference.
Important 'Specific heat' relation (For ideal gas) :
(1) \(C_{p} > C_{v} \)
(2) \(C_{p} - C_{v} = R \) (R can be characteristic or Universal, depends on unit of Cp and Cv)
(3) \( \frac{C_{p}}{C_{v}} = \gamma \)
For Monoatomic gas \( (He, Ar) , \gamma \) = 1.67
For Diatomic gas \((H_{2}, N_{2}) , \gamma \) = 1.4
For Triatomic gas \( (CO_{2}) , \gamma \) = 1.33
(4) \(T\uparrow \Rightarrow C_{p}\uparrow , C_{v}\uparrow , \gamma\downarrow \)
As we know, \( Q = \int{mC_{p}dT} \)
\( Q = \int_{1000}^{300} ( 22.68 + 6.3 \times 10^{-3} T) dT \)
\( Q = -18.74 kJ \)
But as asked Heat released \( \Rightarrow Ans = 18.74 kJ \)
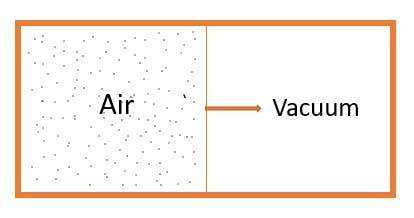
The Image shown above is an special case where in an isolated system ( i.e., \( \delta Q=0 \) ), one side is filled with gas and other kept as vacuum. The wall between them moved infinitely slowly such that work done can be considered zero (i.e., \( \delta W = 0 \))
As from 1st law \( \delta Q = dU + \delta W \Rightarrow dU = 0 \)
\( \Rightarrow U_{i} = U_{f} \)
\( As U = mC_{v}dT \Rightarrow C_{v} T_{i}= C_{v} T_{f} \)
\(\Rightarrow \boxed{ T_{i} = T_{f} } \)
The catch is that we did not started as Isothermal Process but still \(T_{i} = T_{f}\). It Means free expansion process are isothermal process.